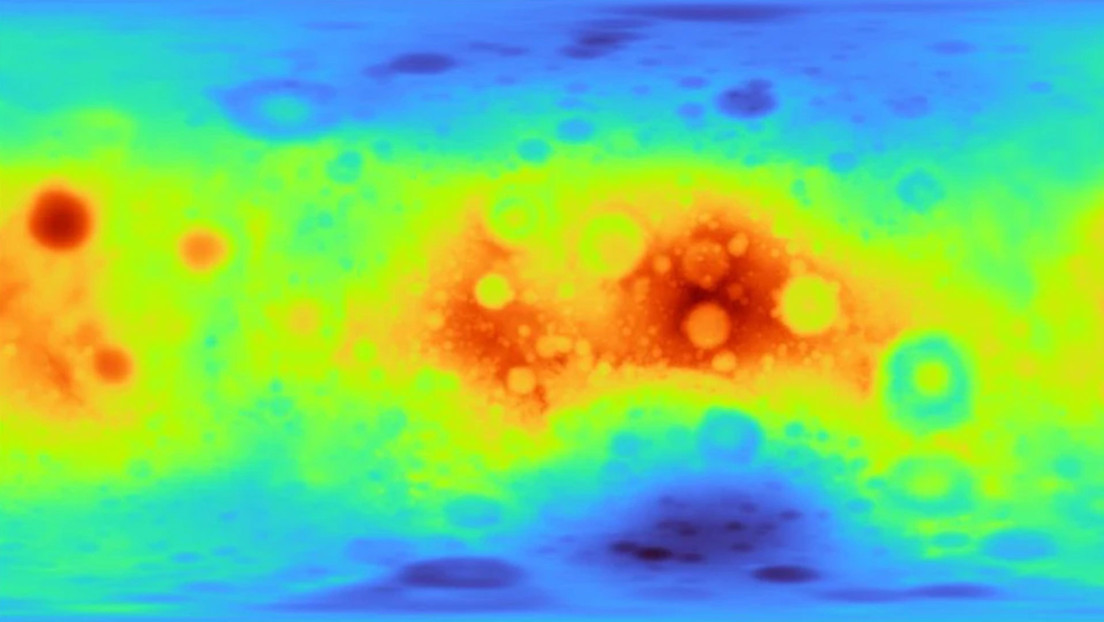
Debido a que la Luna es menos aplanada que la Tierra, el modelo del geoide terrestre no se adapta a su forma teórica. Por esto, el modelo informático que sustenta la navegación por GPS en la Tierra no se puede aplicar a la Luna sin la adecuación necesaria
Investigadores de la Universidad Eötvös Loránd, en Hungría, adaptaron los parámetros utilizados en el sistema GPS de la Tierra para su implementación en la Luna. Los científicos utilizaron un método desarrollado hace más de 8 siglos por el matemático Leonardo Fibonacci con el fin de obtener los parámetros clave necesarios para que los sistemas de navegación satelital terrestres se puedan usar en la superficie lunar.
El modelo del geoide no se adapta a la Luna
Con el renacimiento de las misiones a la Luna, los sucesores modernos de los vehículos lunares de las anteriores misiones probablemente serán asistidos por alguna forma de navegación por satélite, similar al sistema GPS terrestre. En el caso de la Tierra, estos sistemas no tienen en cuenta la forma real de nuestro planeta, el geoide, sino un elipsoide giratorio que se adapta mejor al geoide.
Sin embargo, dado que la Luna es menos aplanada que la Tierra (es casi una esfera, pero no del todo) el modelo del geoide terrestre no se adapta a su forma teórica. Nunca antes se había hecho la aproximación de la forma de la Luna con un elipsoide giratorio, pues cálculos similares que se realizaron en la década de 1960, por científicos espaciales soviéticos, utilizaron solamente datos de la cara visible de la Luna.
¿Qué parámetros son necesarios para la adaptación del modelo?
Para aplicar las soluciones de ‘software’ probadas en el sistema GPS terrestre a la navegación lunar se necesita especificar dos números: el semieje mayor y el semieje menor de este elipsoide. La autora principal, Kamilla Cziráki, y su tutor, Gábor Timár, utilizaron una base de datos de una superficie potencial existente, llamada solenoide lunar, para calcular los valores de estos semiejes.
Ellos tomaron una muestra de altura en puntos espaciados uniformemente en la superficie y buscaron el semieje mayor y el semieje menor que mejor se ajustan a un elipsoide rotatorio. Al aumentar gradualmente el número de puntos de muestreo de 100 a 100.000, los valores de los dos parámetros se estabilizaron en 10.000 puntos.
La esfera de Fibonacci
Un problema fue investigar cómo disponer uniformemente N puntos sobre una superficie esférica, con varias soluciones posibles. Entonces, la esfera de Fibonacci emergió como la solución más simple y óptima al problema. El método también se ha aplicado a la Tierra como verificación, reconstruyendo una buena aproximación del elipsoide WGS84 utilizado por GPS. Los hallazgos de esta investigación se publicaron, recientemente, en Acta Geodaetica et Geophysica.